Shortest Path Graph Algorithms
date : 4th January, 2013
The problem of finding shortest paths, which can also be called `shortest path problem`, is a fundamental problem with numerous applications. The most common applications arise in transportation or communications, such as finding the best route to drive between two cities or figuring how to direct packets to a destination across a network. In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the costs of its constituent edges is minimized.
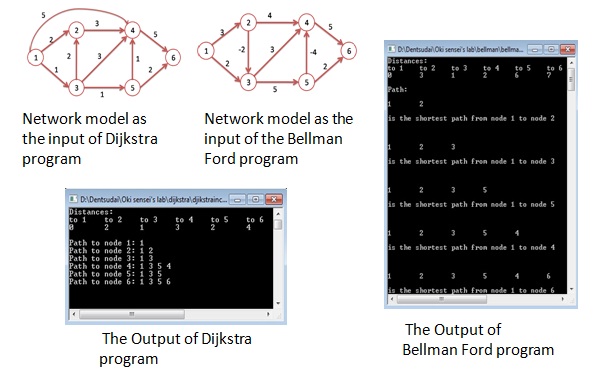
Shortest path graph algorithms are the algorithms used to solve the shortest path problem for a graph. Two of the most important shortest path graph algorithms are Dijkstra’s Algorithm and Bellman-Ford’s Algorithm. Both of those algorithms can be used to solve the single-source shortest path problem, which is to find the shortest paths from a source node to all other nodes in a graph.
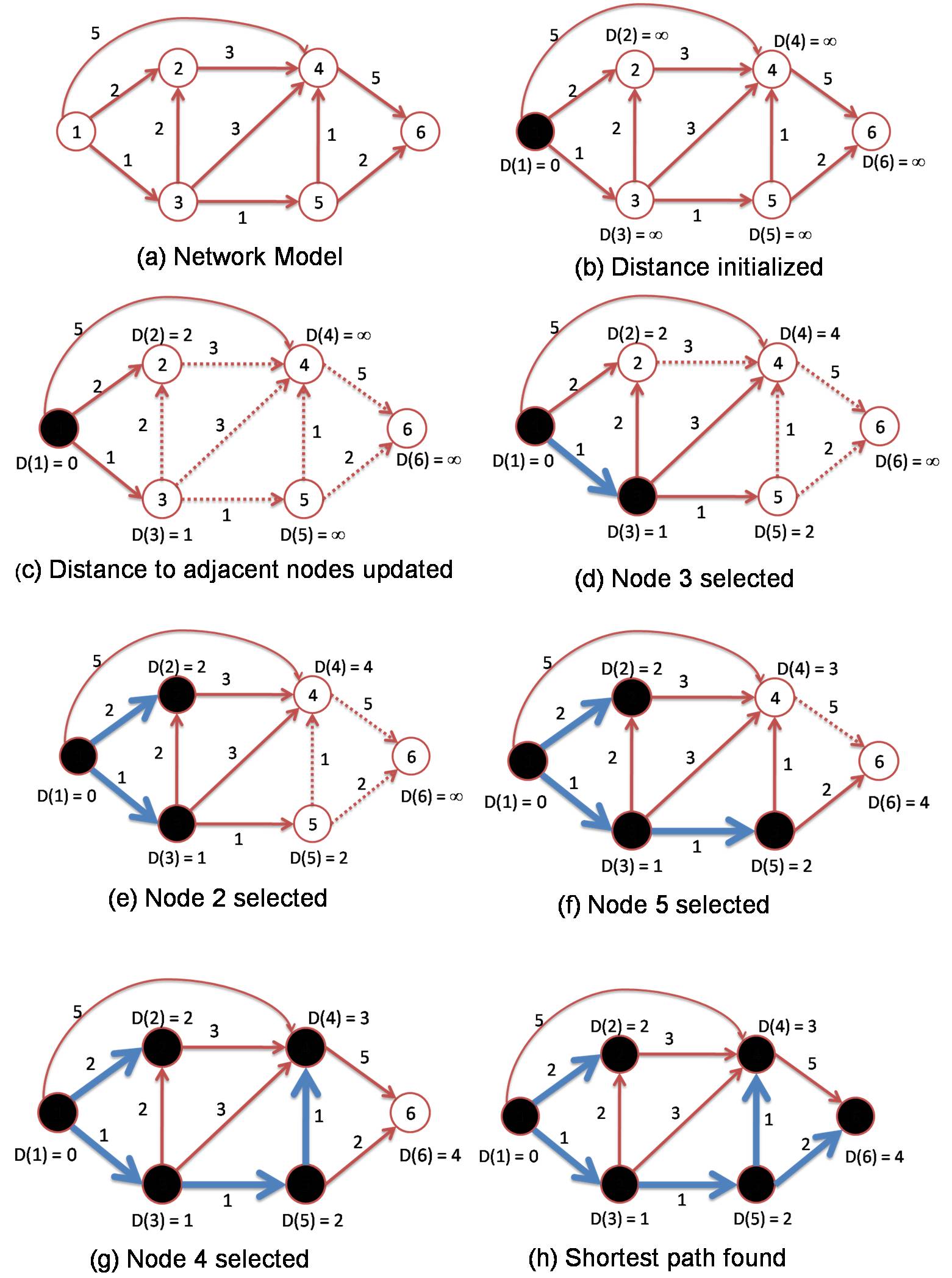
This study about Dijkstra’s Algorithm and Bellman-Ford’s Algorithm is mainly about the working principles of the algorithms when solving the shortest path problem in a graph. In Dijkstra’s Algorithm, nodes in the network are divided into three types of nodes, which are a visiting node, a visited node, and an unvisited node. At the initial stage, the source node is set as a visiting node, and other nodes are set as unvisited nodes. Set the distance to zero for the source node and to infinity for all other nodes. The distance between nodes adjacent to the visiting node are computed by adding the cost of the link between the visiting node and each adjacent node to the distance of the current node. Next, select the next node to visit. Repeat the process until every node in the network becomes a visited node. This process yields the shortest paths from the source node to all nodes in the graph network.
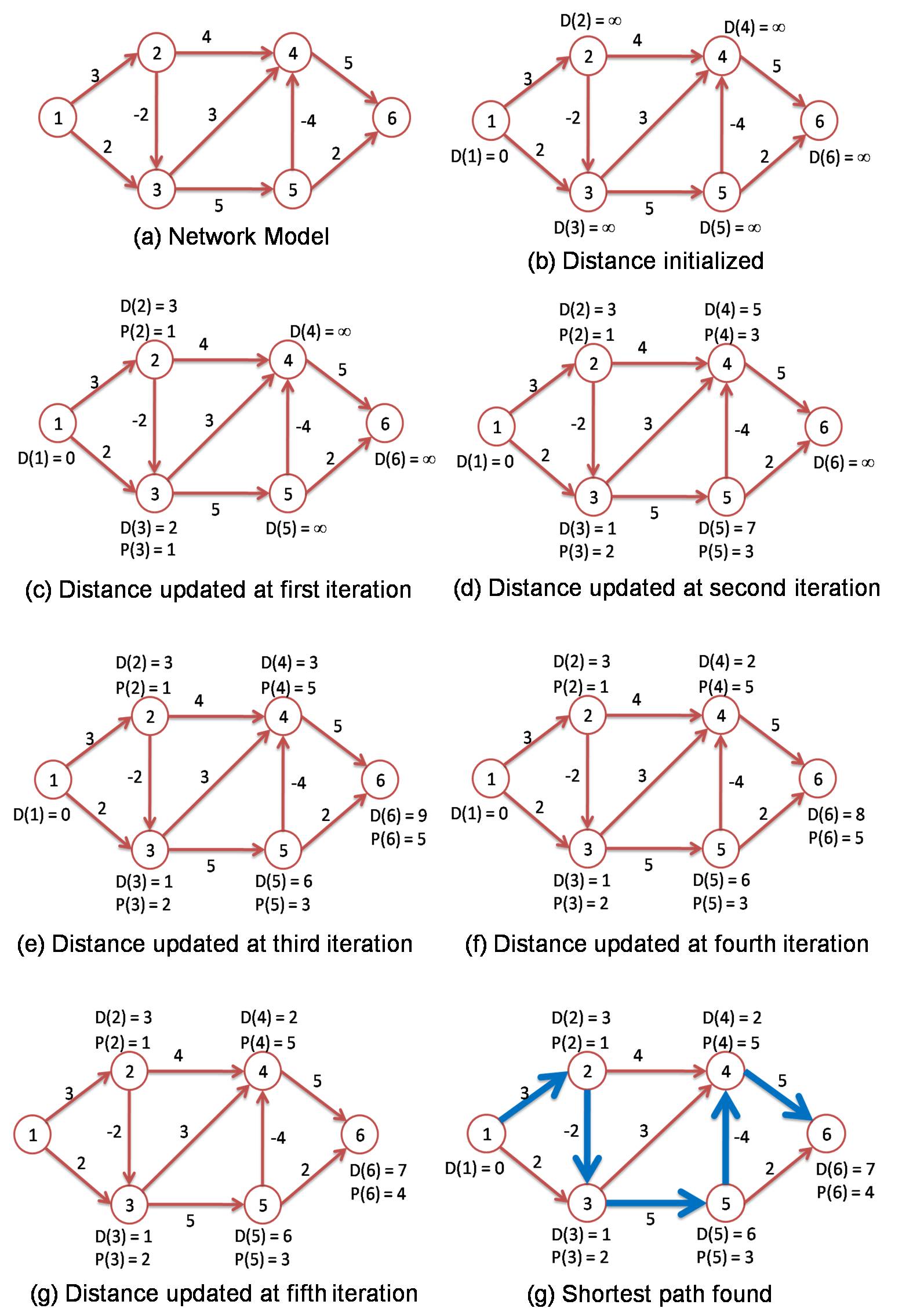
In the Bellman-Ford’s Algorithm, a node is not categorized by visited or not. At the initial stage, set the distance to zero for the source node and to infinity for all other nodes. Then at each node, select an adjacent node so that the summation of the distance of the adjacent node and the cost of the link from the adjacent node to its own node is minimized. Set the selected adjacent node to be the previous hop node to be the previous hop node. The shortest path can be found after repeating the process for N-1 times (N is the number of nodes in the network) .
The implementation of the two algorithms is done in C language to create applications that can be used to solve the shortest path problem of a graph. The input of the application is the information of the graph (amount of nodes, list of costs, list of edges, etc). The output of the application is the shortest path between source node and every other nodes of the input graph.