Page 33 - 2025S

26 UEC Int’l Mini-Conference No.54

Third, we perform comprehensive variant anal-
ysis by rigorously benchmarking five adaptive
configurations across multiple problem domains.
Fourth, we establish novel hypervolume-centric
evaluation metrics specifically designed to as-
sess stability and recovery performance in dy-
namic environments. Collectively, these con-
tributions address critical limitations in exist-
ing approaches while providing new mechanisms
for maintaining solution quality during environ-
mental transitions.

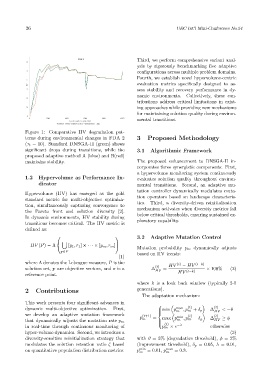
Figure 1: Comparative HV degradation pat-
terns during environmental changes in FDA 2 3 Proposed Methodology
(τ t = 10). Standard DNSGA-II (green) shows
significant drops during transitions, while the 3.1 Algorithmic Framework
proposed adaptive method A (blue) and B(red)
maintains stability. The proposed enhancement to DNSGA-II in-
corporates three synergistic components: First,
a hypervolume monitoring system continuously
1.2 Hypervolume as Performance In- evaluates solution quality throughout environ-
dicator mental transitions. Second, an adaptive mu-
tation controller dynamically modulates muta-
Hypervolume (HV) has emerged as the gold
standard metric for multi-objective optimiza- tion operators based on landscape characteris-
tion, simultaneously capturing convergence to tics. Third, a diversity-driven reinitialization
mechanism activates when diversity metrics fall
the Pareto front and solution diversity [2].
In dynamic environments, HV stability during below critical thresholds, ensuring sustained ex-
transitions becomes critical. The HV metric is ploratory capability.
defined as:
  3.2 Adaptive Mutation Control
[
HV (P) = Λ  [y 1 , r 1 ] × · · · × [y m , r m ] 
Mutation probability p m dynamically adjusts
y∈P based on HV trends:
(1)
where Λ denotes the Lebesgue measure, P is the HV (t) − HV (t−k)
solution set, y are objective vectors, and r is a ∆ (t) = × 100% (2)
HV HV (t−k)
reference point.
where k is a look back window (typically 2-5
2 Contributions generations).
The adaptation mechanism:
This work presents four significant advances in

(t)
dynamic multi-objective optimization. First, min p max , p m + δ p ∆ (t) < −θ
 m HV
we develop an adaptive mutation framework (t+1)  (t) (t)
p m = max p min , p m − δ p ∆ ≥ ϕ
that dynamically adjusts the mutation rate p m  m HV

 (t)
in real-time through continuous monitoring of p m × e −λ otherwise
hyper-volume dynamics. Second, we introduce a (3)
diversity-sensitive reinitialization strategy that with θ = 5% (degradation threshold), ϕ = 2%
modulates the solution retention ratio ζ based (improvement threshold), δ p = 0.05, λ = 0.01,
on quantitative population distribution metrics. p min = 0.01, p max = 0.3.
m
m